ראשי » מטבעות דיגיטליים » הכירו את זיקאש (Zcash) – להוכיח מבלי להראות

הכירו את זיקאש (Zcash)

להוכיח מבלי להראות

זיקאש (Zcash) הוא מטבע קריפטוגרפי מבוזר בעל רשת בלוקצ'יין המאפשרת להשתמש בשתי שכבות שונות: אחת שקופה וגלויה לחלוטין ואחת פרטית ואטומה.
בניגוד לרשתות אחרות, זיקאש מתבסס על "הוכחה באפס ידיעה" (Zero Proof Knowledge). כלומר, הוכחה שלא דורשת מהצד המוכיח לספק מידע על מה שהוא טוען על מנת לשכנע את הצד השני באמיתות הטענה (בהמשך נסביר מהי המשמעות של כך בפועל). באמצעות זיקאש אפשר להסתיר את כל פרטי ההעברה: פרטי השולח, פרטי המקבל והסכום שהועבר. באופן זה (ובניגוד לרשת שקופה כמו ביטקוין), קשה יותר לפורצים לזהות קורבנות פוטנציאלים עם כיסים שמנים על פי תכולת הארנק שלהם והיסטורית ההעברות שלהם. לפיכך, זיקאש יכול להתאים לארגונים שרוצים להשתמש בטכנולוגית הקריפטו בלי לחשוף את הפעילות שלהם בפני הלקוחות, המתחרים או הספקים.

דרגו את Zcash מ-1 עד 5:

הכירו את זיקאש (Zcash) – להוכיח מבלי להראות

ציון: 4/5 (6 מדרגים)

היצע ושווי שוק

שער זיקאש וכמות המטבעות

לזיקאש לא בוצעה הנפקה ראשונית או כרייה מוקדמת (Premine) ולכן הוא מתבסס אך ורק על כרייה, באופן דומה לביטקוין. הבלוק הממוצע נוצר תוך 2.5 דקות ובסופו של דבר מתקבלות 12.5 יחידות Zcash חדשות כגמול לכורה אשר יצר את הבלוק (כלומר, בכל 10 דקות נוצרות 50 יחידות חדשות).

מספר המטבעות המקסימלי שניתן לכרות הוא 21 מיליון, אך בכל ארבע שנים חל תהליך של חציית בלוקים, והגמול לכורים יורד במחצית (בדומה לביטקוין).

נכון לעכשיו, ישנם בסירקולציה כ-6.6 מיליון מטבעות. את הערך המעודכן של המטבע ניתן לראות בתיבה למעלה בצד שמאל.

Zcash

Price
53.8565786949

Supply 8.70M ZEC

Volume 293.06M

Market Cap 468.78M

Change 9.77%

צוות הפיתוח

מי עומד מאחורי מטבע זיקאש

צוות הפיתוח של זיקאש מורכב ממדענים, מהנדסים, מעצבים ואנשי עסקים מקצועיים ממוסדות נחשבים ברחבי העולם: ביניהם MIT, אוניברסיטת ג'ונס הופקינס וגם אוניברסיטאות תל אביב והטכניון הישראליים. מרבית החברים בקבוצה הזו היו גם חלק מהקבוצה שפיתחה את הפרוטוקול על פיו בנויה הרשת ונקרא באופן לא מפתיע מאוד זירוקוין (Zerocoin).

ראש הקבוצה, זוקו וילקוקס (Zooko Wilcox), הוא בעל ניסיון של יותר מ-20 שנה בעבודה עם מערכות פתוחות ומבוזרות, אבטחת מידע, קריפטוגרפיה וסטארט-אפים שונים.

לצרכי פיתוח זיקאש הוקמה עמותה ללא מטרות רווח הנקראת 'Zcash Foundation'. בכדי לממן את הפעילות השוטפת, 10% מהגמול לבלוק במשך 4 שנותיה הראשונות של הרשת יופנו ל-'Founders Reward'. כלומר, אם כיום עבור כריית בלוק הכורה מקבל 12.5 מטבעות, 1.25 מהם עוברים לניהולה של הקרן. ה-10% הללו מחולקים בצורה הבאה:

1.65% יועברו למשקיעים מוקדמים בפרויקט כגון קרן ההשקעות Pantera, קבוצת Digital Currency Group, רוג'ר וור, אדם לודווין ועוד.
5.72% יועברו למפתחים, מייסדים ועובדים.
1.19% יישמרו כרזרבה אסטרטגית ל-'Zcash Company'.
1.44% לניהולה השוטף של הקרן.

איך זה עובד?

איך עובד מטבע זיקאש

במסגרת העברה של ZEC (המטבע של Zcash), שני הצדדים יכולים לבחור האם להשתמש בכתובת רגילה (T-address) או בכתובת מוגנת (Z-address). השימוש ב-T-address למעשה נותן לנו טרנסקציה רגילה, כמו של ביטקוין, ואילו השימוש בכתובת המוגנת מאפשר להסתיר לחלוטין את הטרנסקציה. אם רק אחד מהצדדים בוחר להסתיר את הכתובת שלו, זוהי העברה מוגנת למחצה.

תהליך הכרייה של Zcash ופרדוקס יום ההולדת

אלגוריתם הכרייה של זיקאש נקרא Equihash והוא מבוסס על הוכחת העבודה (Proof of Work) ובעיה קלאסית בסטטיסטיקה המוכרת בתור "פרדוקס יום ההולדת". הפרדוקס מתאר מצב שבו שני זרים מוחלטים נפגשים ברחוב ומסתבר שהם נולדו באותו יום. מכיוון שיש 365 ימים בשנה, הסבירות לכך היא 0.27%. לעומת זאת, אם ישנם 20 עד 30 איש באותו חדר, הסיכוי שלשניים מהם יהיה יום הולדת באותו תאריך עולה באופן דרמטי ל-50%!

מדוע זה קורה? חוק בסיסי בתורת ההסתברות קובע שאם יש N אפשרויות להתרחשות של אירוע מסוים, צריך את השורש הריבועי של N עצמים כדי שיהיה סיכוי של 50% להתנגשות ביניהם. במקרה של פרדוקס יום ההולדת, אנחנו זקוקים לשורש הריבועי של 365, כלומר 23 איש.

אופי הבעיה הזו מונע מצב שבו כורים עם חומרה ייעודית (ASIC) יוכלו לקבל יתרון על כורים עם חומרה חלשה יותר. אם תהליך הכרייה עובר אופטימיזציה, כולם יכולים ליהנות ממנה.

הוכחות באפס ידיעה (Zero-Knowledge Proofs)

הוכחה באפס ידיעה הוא קונספט במדעי המחשב שפותח עוד בשנות השמונים. הקונספט מתאר מצב שבו מי שנושא עליו את נטל ההוכחה צריך לשכנע גורם אחר באמיתות הטענה בלי שהוא חושף את מה שהוא יודע.

למעשה, במקום לבדוק האם הטענה היא שקרית, הבדיקה נועדה למנוע מצב שבו מי שמאמת את הטענה ידליף את המידע הלאה. לכן, המטרה היא לחשוף אותו לכמה שפחות מידע.

אפשר לקחת דוגמה פשוטה של הכנסת סיסמה לשם כניסה לאתר: אפילו אם הסיסמה מוצפנת במסד הנתונים, המשתמש עצמו מקליד את הסיסמה הלא מוצפנת והשרת מקבל אותה, מה שעלול לחשוף אותה לפורצים.

להוכחה באפס ידיעה יש שני צדדים – 'מוכיח' (Prover) ו-'מאמת' (Verifier). כדי שההוכחה תעבוד, חייבים להתקיים שלושה תנאים עבור ההצהרה שאותה רוצים להעביר בין הצדדים:

שלמות – אם ההצהרה נכונה, אז 'מאמת' הגון יכול להיות משוכנע על ידי 'מוכיח' הגון.
תקפות – אם מי שמוכיח את ההצהרה הוא לא הגון, הוא לא יכול לשכנע את מי שמאמת את הצהרה באמצעות שקר.
אפס ידיעה – אם ההצהרה נכונה, ל'מאמת' לא יהיה מושג מה ההצהרה אומרת.

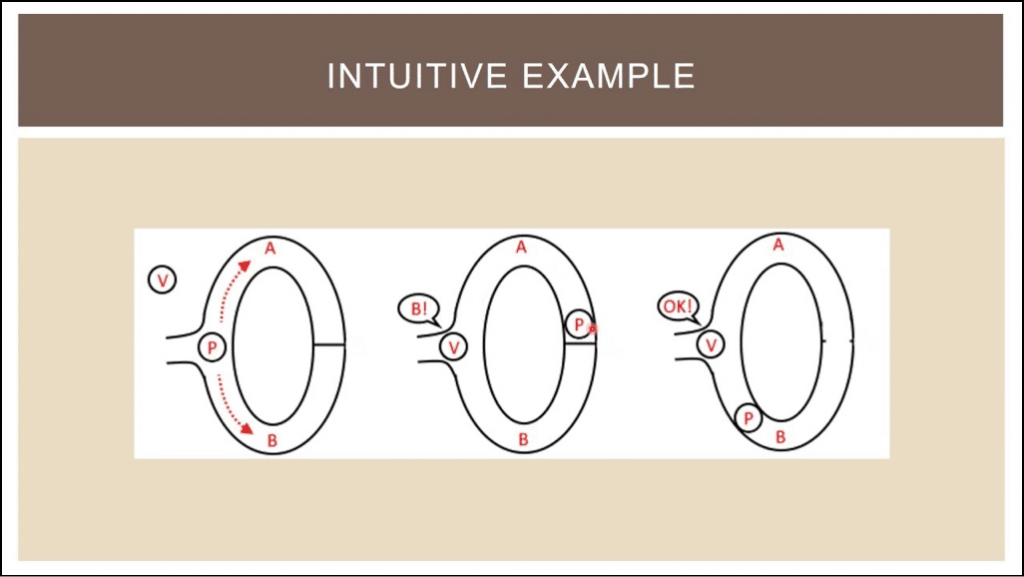
אחת הדוגמאות הידועות שמדגימות את הרעיון היא 'המערה של עליבאבא': נניח שקיימת מערה בצורת המספר "0" ולה יש דלת אחורית עם סיסמה. כיצד מי שיודע את הסיסמה לדלת האחורית למערה יכול להוכיח למישהו אחר שהוא יודע אותה, מבלי למסור לו אותה?

אך מה אם היה מדובר במזל? מה אם ה'מוכיח' לא ידע את הסיסמה לדלת האחורית, בחר בנתיב B ובמזל רב ה'מאמת' בחר לבקש שיגיע מנתיב B?
ובכן, מהכניסה הקדמית אפשר לקחת את נתיב A או נתיב B כדי להגיע לדלת האחורית (המערה השמאלית בדוגמה). נניח שה'מוכיח' (המסומן בעיגול עם האות 'P') בוחר בנתיב A ומגיע לדלת הסודית שבצד השני (המערה האמצעית). כשהוא מגיע לדלת הסודית, ה'מאמת' (מסומן באות 'V'), שלא ראה את נתיבו של ה'מוכיח' בתוך המערה, צועק לו "אני רוצה שתגיע מנתיב B!". ה'מוכיח' מגיע מנתיב B ועל פניו נראה שהצליח להוכיח לו.

אם כן, בכדי לבחון את אימות הטענה, הניסוי מתבצע כמה וכמה פעמים. אם ה'מוכיח' מגיע בנתיב הנכון כל פעם – זה מוכיח ל'מאמת' שהוא אכן יודע את הסיסמה לדלת האחורית, למרות שה'מאמת' לא יודע אותה בעצמו.

כיצד שלושת העקרונות משתלבים כאן?

שלמות – כיוון שהטענה נכונה, ה'מוכיח 'ההגון הצליח לשכנע את ה'מאמת' ההגון.
תקפות – אם ה'מוכיח' לא היה הגון וחזר על המבחן כמה פעמים, בשלב מסוים, היה אמור להיגמר לו המזל והוא היה נתפס על חם.
אפס ידיעה – ה'מוכיח' הצליח לשכנע את ה'מאמת' גם בלי שחשף בפניו את הסיסמה.

החשיבות של ה-Zk-Snarks

Zk-Snarks הם ראשי תיבות של "Zero-Knowledge Succinct Non-Interactive Argument of Knowledge" והם למעשה המימוש של הוכחות באפס מידע בתוך החוזים החכמים של זיקאש. בזכותם ניתן לבצע העברות בטוחות של מטבעות או סחורות אחרות מבלי לחשוף את פרטי התהליך לגורמים מבחוץ.

יתרונות וחסרונות

היתרונות והחסרונות של מטבע זיקאש

בראש ובראשונה, העובדה שצוות הפיתוח מגיע ברובו הגדול ממוסדות ההשכלה הגבוהה הופך את Zcash לפיתוח בסטנדרט מדעי גבוה יותר מאשר הפיתוח הממוצע בסצנה וההישג שלו עם Zk-Snarks נחשב לפריצת דרך של ממש בתחום הקריפטוגרפיה.

ייתכן שהיתרון התדמיתי הזה הוא זה אשר גרם לתאגיד הענק JPMorgan להטמיע את הטכנולוגיה של זיקאש בתוך טכנולוגיית הבלוקצ'יין המקבילה שלו, קווארום (Quorum).

למרות היכולת לבצע העברות בטוחות, מסתבר שכמעט 20% מן ההעברות הן העברות שבהן אחד הצדדים חושף את הכתובת שלו, ורק כ-2% מן ההעברות הן מוגנות לחלוטין. במילים אחרות, ניתן לקשר אל כמעט כל ההעברות הקיימות ולחשוף אותן. כמו כן, וכפי שאפשר יהיה לראות מיד, העברות בטוחות דורשות שימוש בארנקים ספציפי.

בנוסף, לאחרונה חלות התפתחויות בתחום הרגולציה עם התמקדות יתרה בזיקאש ובמטבעות אנונימיים נוספים כגון מונרו ודאש. כחלק מהרצון לפעול בציות לרגולציה, בורסות שונות ברחבי העולם החלו להוריד את שווקי המסחר המכילים את המטבעות האנונימיים המובילים , מה שצפוי להקטין את הדרכים האפשריות לרכוש את המטבעות.

מעבר לזאת, ישנו דיון מתמשך הנוגע לסוגיית ה-Founders Reward בזיקאש. בעוד שהקהילה מעוניינת לתגמל את המפתחים והמייסדים על ניסיונותיהם ליצור כסף מזומן דיגיטלי אנונימי ומבוזר, יש שאומרים ש-2.1 מיליון מטבעות זה הרבה מדי, ושהחלוקה איננה הוגנת.

לבסוף, בחודש פברואר 2019 התגלה באג חמור בקוד התוכנה של המטבע. הבאג אפשר לתוקף פוטנציאלי ליצור מטבעות ZEC חדשים יש מאין. לאור מאפייני המטבע, אין דרך לדעת האם תוקף מסוים הספיק לנצל את הבאג, אך לאור המורכבות המתמטית הנדרשת כדי לזהותו – ההערכות של המומחים המעורבים מדברות על סיכויים נמוכים עד בלתי אפשריים.

ארנקים מומלצים

ארנק זיקאש מומלץ

הארנקים בהם ניתן להחזיק את המטבע ZEC מתחלקים לשניים: כאלו שמאפשרים העברות שקופות (רגילות) בלבד וכאלו שמאפשרים גם או רק העברות מוגנות.

ארנקים ללא העברות מוסתרות

ארנקי חומרה – שני ארנקי החומרה המובילים טרזור (Trezor) ולדג'ר ננו אס (Ledger Nano S) נחשבים כיום לארנקים המאובטחים ביותר ולפיכך הם המומלצים ביותר. ארנק חומרה הוא ארנק דיגיטלי קר, כלומר כזה שאיננו מחובר לרשת האינטרנט, כך שהוא מאפשר ניתוק מוחלט בין המפתחות הפרטיים לבין גורמים זדוניים אשר ינסו להשתלט עליהם.
Guarda (מובייל ו-WEB) – הארנק מאפשר לבצע עסקאות ב-ZEC בגרסת האנדרואיד והווב שלו (קיימת גם גרסה למכשירי אפל). הארנק מאפשר לבצע עסקאות ישירות מול משתמשים אחרים ולקנות את המטבע עם כרטיס אשראי. הארנק גם מוגן באמצעות קוד PIN אישי והמפתחות של המשתמשים נשארים מוסתרים.
ארנק ג'קס (Jaxx) – ארנק ידוע ומוכר שקל להשתמש בו אך קוד התוכנה שלו סגור חלקית מה שמהווה חיסרון גדול. עדיף שתקראו את הסקירה המלאה על ארנק ג'קס ותחליטו בעצמכם, משום שבעינינו חווית המשתמש לא צריכה לבוא על חשבון האבטחה.

ארנקים עם העברות מוסתרות

WinZEC – ארנק עבור מערכת הפעלה ווינדוס, בעל קוד פתוח ולמעשה מדובר בהרצת צומת מלא על גבי מחשביכם (כך שדרוש הליך סנכרון די ארוך).
הרצת Zcash בסביבת לינוקס – הקישור מהווה מדריך מלא להרצת צומת מלא על גבי מערכת ההפעלה לינוקס.
kozyilmaz – הקישור מהווה מדריך מלא להרצת צומת מלא על גבי מערכת ההפעלה מק.

קניית זיקאש

איך קונים זיקאש?

ישנן מספר דרכים שונים לרכישת המטבע ZEC:

זירות מסחר

בינאנס (Binance)

זירת המסחר הסינית הגדולה ביותר בשוק המטבעות הדיגיטליים. בעלת הממשק הנוח ביותר ונפח המסחר הגבוה ביותר. למדריך מלא על בינאנס.

קוקוין (KuCoin)

זירות מסחר אשר ניתן לבצע את הרכישה דרכה. למדריך המלא על בורסת קוקוין.

חלפנים

צ’יינג’לי (Changelly)

(Changelly) – חלפן הכספים המאפשר לבצע המרת קריפטו לקריפטו דרכו. קל יותר לשימוש ומהיר מבינאנס, אבל עם עמלות מעט גבוהות יותר. בנוסף, הכנו עבורכם את המדריך המלא לחלפן הקריפטו צ'יינג'לי.

שייפשיפט (ShapeShift)

חלפן קריפטו לקריפטו ככל הנראה המפורסם ביותר בתעשייה כיום, וניתן לרכוש דרכו ZEC באמצעות ביטקוין, את'ר ואף מטבעות אחרים. למדריך המלא על שייפטשיפט.

אנשים פרטיים

הדרך האחרונה האפשרית לרכישת זיקאש היא דרך אנשים פרטיים. קיימות כיום קבוצות פייסבוק או טלגרם המפגישות בין מוכרים לקונים כך שמבצעים את ההעברה ישירות מבלי לעבור דרך גורם מתווך. היתרון בשיטה זו הם שלרוב יהיה מדובר ברכישה ללא עמלות, אם כי החיסרון הוא שקיימים לא מעט מקרי הונאה.

במאמר הבא על 'איך קונים ביטקוין במזומן' פירטנו עבורכם גם על הקבוצות הרלוונטיות, וגם על החוקים שחשוב לקחת בחשבון.